Poligon Tertutup
PENGANTAR ILMU UKUR TANAH (POLIGON)
POLIGON
Kerangka Kontrol Horisontal (KKH) merupakan kerangka dasar pemetaan
yang memperlihatkan posisi horisontal (X,Y) antara satu titik relatif
terhadap titik yang lain di permukaan bumi pada bidang datar. Untuk
mendapatkan posisi horisontal dari KKH dapat digunakan banyak metode,
salah satu metode penentuan posisi horisontal yang sering digunakan
adalah metode poligon. Metode poligon digunakan untuk penentuan posisi
horisontal banyak titik dimana titik yang satu dan lainnya dihubungkan
dengan jarak dan sudut sehingga membentuk suatu rangkaian sudut
titik-titik (polygon). Pada penentuan posisi horisontal dengan metode
ini, posisi titik yang belum diketahui koordinatnya ditentukan dari
titik yang sudah diketahui koordinatnya dengan mengukur semua jarak dan
sudut dalam poligon.
Macam-macam Poligon
Poligon dapat dibedakan berdasarkan dari [1] bentuk dan [2] titik ikatnya.
- Poligon Menurut Bentuknya
Berdasarkan bentuknya poligon dapat dibagi menjadi empat macam, yaitu :
- poligon terbuka,
- tertututup,
- bercabang dan
- kombinasi.
- Poligon Terbuka
Poligon terbuka adalah poligon yang titik awal dan titik akhirnya
merupakan titik yang berlainan (tidak bertemu pada satu titik).
- Poligon Tertutup
Poligon tertutup atau kring adalah poligon yang titik awal dan
titik akhirnya bertemu pada satu titik yang sama. Pada poligon tertutup,
koreksi sudut dan koreksi koordinat tetap dapat dilakukan walaupun
tanpa titik ikat.
- Poligon Bercabang
Poligon cabang adalah suatu poligon yang dapat mempunyai satu atau lebih titik simpul, yaitu titik dimana cabang itu terjadi.
- Poligon Kombinasi
Bentuk poligon kombinasi merupakan gabungan dua atau tiga dari bentukbentuk poligon yang ada.
2. Poligon Menurut Titik Ikatnya
1. Poligon Terikat Sempurna
Suatu poligon yang terikat sempurna dapat terjadi pada poligon
tertutup ataupun poligon terbuka, suatu titik dikatakan sempurna sebagai
titik ikat apabila diketahui koordinat dan jurusannya minimum 2 buah
titik ikat dan tingkatnya berada diatas titik yang akan dihasilkan.
- Poligon tertutup terikat sempurna :
Poligon tertutup yang terikat oleh azimuth dan koordinat.
- Poligon terbuka terikat sempurna :
Poligon terbuka yang masing-masing ujungnya terikat azimuth dan koordinat.
2. Poligon Terikat Tidak Sempurna
Suatu poligon yang terikat tidak sempurna dapat terjadi pada
poligon tertutup ataupun poligon terbuka, dikatakan titik ikat tidak
sempurna apabila titik ikat tersebut diketahui koordinatnya atau hanya
jurusannya.
- Poligon tertutup tidak terikat sempurna :
Poligon tertutup yang terikat pada koordinat atau azimuth saja.
- Poligon terbuka tidak terikat sempurna :
- Poligon terbuka yang salah satu ujungnya terikat oleh azimuth saja, sedangkan ujung yang lain tidak terikat sama sekali. Poligon semacam ini dapat dihitung dari azimuth awal dan yang diketahui dan sudut-sudut poligon yang diukur, sedangkan koordinat dari masingmasing titiknya masih lokal.
- Poligon terbuka yang salah satu ujungnya terikat oleh koordinat saja, sedangkan ujung yang lain tidak terikat sama sekali.Poligon semacam ini dapat dihitung dengan cara memisalkan azimuth awal sehingga masing-masing azimuth sisi poligon dapat dihitung, sedangkan koordinat masing-masing titik dihitung berdasarkan koordinat yang diketahui. Oleh karena itu pada poligon bentuk ini koordinat yang dianggap betul hanyalah pada koordinat titik yang diketahui (awal) sehingga poligon ini tidak ada orientasinya.
- Poligon terbuka yang salah satu ujungnya terikat oleh azimuth dan koordinat, sedangkan ujung yang lain tidak terikat. Poligon jenis ini dapat dikatakan satu titik terikat secara sempurna namun belum terkoreksi secara sempurna baik koreksi sudut maupun koreksi koordinat, tetapi sistim koordinatnya sudah benar.
- Poligon terbuka yang kedua ujungnya terikat oleh azimuth. Pada poligon jenis ini ada koreksi azimuth, sedangkan koordinat titik-titik poligon adalah koordinat lokal.
- Poligon terbuka yang kedua ujungnya terikat oleh koordinat. Jenis poligon ini tidak ada koreksi sudut tetapi ada koreksi koordinat.
- Poligon terbuka yang salah satu ujungnya terikat oleh koordinat, sedangkan ujung yang lain terikat azimuth. Pada poligon ini tidak ada koreksi sudut dan koreksi koordinat.
- Poligon terbuka yang salah satu ujungnya terikat oleh azimuth dan koordinat saja, sedangkan ujung yang lain terikat koordinat. Jenis poligon ini tidak ada koreksi sudut tetapi ada koreksi koordinat.
- Poligon terbuka yang kedua ujungnya terikat oleh azimuth dan koordinat, sedangkan ujung yang lain tidak terikat azimuth. Poligon ini ada koreksi sudut tetapi tidak ada koreksi koordinat.
- Poligon terbuka yang kedua ujungnya terikat oleh azimuth dan koordinat, sedangkan ujung yang lain tidak terikat azimuth. Jenis poligon ini ada koreksi sudut tetapi tidak ada koreksi koordinat.
- Poligon tertutup tanpa ikatan sama sekali (poligon lepas)
- Poligon terbuka tanpa ikatan sama sekali (poligon lepas), pengukuran seperti ini akan terjadi pada daerah-daerah yang tidak ada titik tetapnya dan sulit melakukan pengukuran baik dengan cara astronomis maupun dengan satelit. Poligon semacam ini dihitung dengan orientasi lokal artinya koordinat dan azimuth awalnya dimisalkan sembarang.
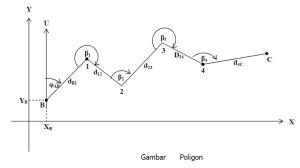
Pada Gambar 9.5, untuk mendapatkan koordinat titik 1, 2, 3 dan 4
maka dilakukan pengukuran sudut (β1, β2,β3, β4) dan jarak (dB1, d12,
d23, d34, d4C)
Rumus koordinat secara umum :
Syarat Geometris Hitungan Koordinat
1. Syarat Sudut
Apabila dipakai pada poligon tertutup dimana titik awal dan titik akhir sama maka rumus diatas akan berubah :
Untuk poligon tertutup yang diukur sudut dalamnya maka :
Untuk poligon tertutup yang diukur sudut luarnya maka :
- syarat sudut :

- syarat ordinat

Toleransi Pengukuran
Cara Pengukuran
- Memasang alat theodolit pada titik awal dan aturlah alat tersebut.
- Posisi teropong biasa arahkan alat pada titik sebelumnya (titik tetap, bila ada) dan kemudian pada titik selanjutnya, putarlah teropong pada posisi luar biasa arahkan ke titik seperti pada posisi teropong biasa.
- Ukurlah jarak antar titik secara langsung dengan pita ukur.
- Kemudian pindahkan alat theodolit ke titik selanjutnya, lakukan langkah 1 s.d 3, demikian seterusnya sampai titik terakhir apabila poligon terbuka dan kembali ke titik awal apabila poligon tertutup.
Cara Perhitungan :
- Hitunglah azimuth awal dan akhir apabila diketahui.
- Hitunglah salah penutup sudut.
- Koreksikan masing-masing sudut pengukuran.
- Hitunglah azimuth masing-masing titik/arah.
- Hitunglah selisih absis (ΔX ) dan selisih ordinat (ΔY )
- Hitung salah penutup absis dan salah penutup ordinat.
- Koreksikan masing-masing selisih absis dan selisih ordinat.
- Hitung koordinat masing-masing titik.









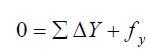





Komentar
Posting Komentar